|
Gráficos de la tortuga
El objetivo de esta práctica es realizar una biblioteca que implemente los
gráficos de la tortuga en Haskell usando la librería AP.GUI.
Ejemplo
import AP.GUI (rgb)
import Turtle
main :: IO ()
main = runTurtle exTree
exTree :: Program
exTree = sub [ rotLeft 90
, retro 180
, tree 90 (drop 3 colors) 6
]
where
tree n (c:cs) w
| n < 5 = noOp
| otherwise = sub [ penColor c
, penWidth w
, forward n
, rotLeft x
, tree'
, rotRight (x+y)
, tree'
, rotLeft y
, retro n
]
where
tree' = tree (n*3/4) cs (max 1 (w-0.75))
x = 30
y = 40
retro :: Unit -> Program
retro n = sub [ penUp, backward n, penDown ]
colors :: [Color]
colors = cycle [ rgb r g b | (r,g,b) <- cs ]
where
cs = [ (255-x,x,0) | x <- ss ]
++ [ (0,255-x,x) | x <- ss ]
++ [ (x,0,255-x) | x <- ss ]
ss = [0,20..255]

Ejercicios
Para esta práctica, como mínimo debes entregar los apartados 1 a 4 (inclusive). A la hora de corregir la
práctica, el profesor valorará, además de los apartados completados, su correcto funcionamiento, junto con
la calidad y claridad del código. Especialmente se valorará la descomposicón del programa en
funciones de modo adecuado, la reutilización de código y el uso de características de
Haskell como las funciones de orden superior, las listas por compresión, etc.
[Aquí] puedes descargar un prototipo para que lo completes.
-
La biblioteca debe definir los siguientes tipos
type Unit = Double
type Degrees = Double
data Command = Forward Unit Command
| RotRight Degrees Command
| Stop
type Program = Command -> Command
donde Unit representa unidades de avance y Degrees ángulos, en grados
sexagesimales, para el avance y giro de la tortuga respectivamente. La biblioteca también
debe implementar los siguientes comandos para describir los movimientos de
la tortuga:
Además, debe implementar una función runTurtle :: Program -> IO () que genere una ventana en la que se visualice el gráfico
generado por la tortuga al ejecutar un programa.
-
Añade los siguientes tipos y comandos al lenguaje de la tortuga
data PenPosition = Up | Down deriving Eq
-
penUp :: Program: levanta el pincel de la tortuga, de modo que al moverse ésta no pinta
-
penDown :: Program: baja el pincel de la tortuga, de modo que al moverse ésta pinta
-
Añade el comando penColor :: Color -> Program que cambie el color con el que pinta la tortuga. Puedes
pintar una línea, por ejemplo roja, entre los puntos p0 y p1 (donde p0, p1 :: Point) del siguiente modo:
line [p0,p1] [color =: red] canv
-
Añade el comando penWidth :: Width -> Program (El tipo Width debes definirlo como un Float) que cambie el ancho
con el que pinta la tortuga. Puedes
pintar una línea, por ejemplo roja de ancho 10, del siguiente modo:
line [p0,p1] [outlineWidth =: 10, color =: red] canv
line [p0,p1] [outlineWidth =: 10, color =: red] canv
-
Añade el comando (<|>) :: Program -> Program -> Program de modo que p1 <|> p2 ejecuta primero p1 y luego p2 desde el estado previo a la ejecución de p1, es decir,
previamente a ejecutar p2 se restaurará la posición, orientación, color, etc. de la tortuga a los valores
que tenían antes de ejecutar p1.
-
Añade el comando pause :: Program. Para implentar este comando añade un botón "seguir" a la interfaz gráfica. Este botón
estará en principio desactivado. Cuando la tortuga ejecute el comando pause se detendrá temporalmente el programa y se activará el botón. Cuando el
usuario pulse el botón "seguir", la tortuga continuará y volverá a desactivarse el botón.
-
Realiza alguna extensión que se te ocurra al lenguaje de la tortuga. Documenta los nuevos comandos
que incorpores y realiza algún ejemplo con ellos.
-
Realiza algún dibujo utilizando la biblioteca que has diseñado.
[Aquí] hay algunos ejemplos para probar tu implementación.
main01 = runTurtle flower
main02 = runTurtle sphere
square n = rept 4 [forward n, rotRight 90]
flower = rept 24 [rotRight 15, square 100]
sphere = rept 12 [ l, rept 12 [f,l] ]
where
l = rotLeft 30
f = forward 30


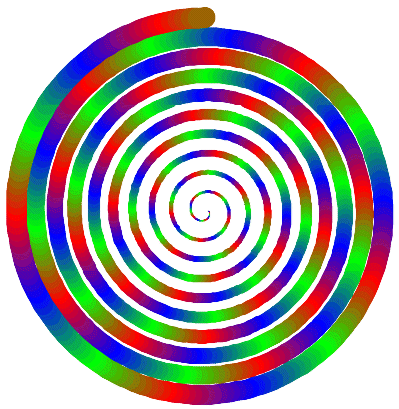
main06 = runTurtle (spiral 0 2 1 colors)
main07 = runTurtle (spiral 0 3 10 colors)
spiral :: Unit -> Degrees -> Width -> [Color] -> Program
spiral size angle w (c:cs)=
if size > 9 then stop
else sub [ penWidth w
, penColor c
, forward size
, rotRight angle
, spiral (size + 0.005) angle (w+0.015) cs
]
main13 = runTurtle exTree3
exTree3 = sub [ rotLeft 90
, retro 150
, tree 200 (drop 3 colors) 4
]
where
tree n (c:cs) w
| n < 5 = noOp
| otherwise = let
subTree distance scale rotation =
sub [ advance (distance*n)
, rotation
, tree (scale*n) cs (max 1 (w-0.75))
]
in
sub [ penColor c
, penWidth w
, forward n
<|>
subTree 0.60 0.76 (rotRight 35)
<|>
subTree 0.55 0.33 (rotRight 45)
<|>
subTree 0.40 0.50 (rotLeft 60)
]

main04 = runTurtle (f1 10)
main05 = runTurtle (f3 10)
fractal :: Program -> [Program] -> Int -> Program
fractal p0 xs n = sub [ retro 100, fractal' p0 xs n ]
where
fractal' p0 xs 0 = p0
fractal' p0 xs n = sub [ sub [x, fractal' p0 xs (n-1)] | x <- xs]
f1 = fractal (forward 4) [noOp, rotRight 90, rotLeft 90, rotLeft 90, rotRight 90]
f3 = fractal (forward 4) [noOp,rotRight 300,rotRight 120,rotRight 300]


main11 = runTurtle (sierpinski 5)
sierpinski n = sub [ sier n dx, r, b, l, l, b ]
where
dx = 200
b = backward dx
f = forward dx
r = rotRight 60
l = rotLeft 60
sier n dx
| n == 0 = forward dx
| otherwise = sub [ s, r, b, l, s
, l, b, r, s
]
where
dx' = dx / 2
s = sier (n-1) dx'
b = backward dx'

|