![]()
ALGORITMOS PARALELOS
![]()
Hoy en día existe una gran cantidad de aplicaciones que requieren el procesamiento de grandes volúmenes de datos en un pequeño margen de tiempo, hasta tal punto que no existen equipos lo suficientemente rápidos para estas operaciones.
El problema al que nos enfrentamos es de tipo físico: la velocidad de la luz. Si su velocidad es de 3x108m/s y suponiendo que un dispositivo electrónico realice 1012 operaciones por segundo, una señal que se envíe desde un dispositivo que se encuentre a 0.5 mm, tardará más en llegar que en ser procesada, formándose entonces una cola de tareas.
Una posible solución sería unir componentes evitando espacios entre ellos. Pero la solución no es factible, ya que estos se podrán acercar hasta el punto en que empiecen a interactuar, lo que hace perder tanto velocidad como fiabilidad.
La única solución posible es la de realizar varias operaciones a la vez; la división de tareas.
Un ordenador paralelo consta de varias CPU's o procesadores que divide las tareas en subtareas que ejecuta en cada uno de sus procesadores de forma simultánea, para luego unir los resultados y obtener una solución al problema original.
Un algoritmo paralelo es una forma concreta de solucionar un problema en un ordenador paralelo. Pero para la obtención de este algoritmo es necesario conocer a fondo el modelo computacional que sigue el ordenador.
![]()
Los ordenadores se pueden clasificar según la secuencia de instrucciones y el conjunto de datos que maneje:
Single Instruction, Single Data. Es el modelo que sigue la mayoría de los ordenadores. Son equipos con un único procesador en los que se procesan algoritmos secuenciales sobre un conjunto de datos. Se ejecutan los pasos uno a uno, no haciendo uso del paralelismo.

Multiple Instruction, Single Data. En este modelo los ordenadores disponen de N procesadores, cada uno con su unidad de control que comparten una unidad de memoria. Estos procesadores operan simultáneamente. Aunque todos los procesadores operen sobre los mismos datos pueden realizar operaciones diferentes.

Single Instruction, Multiple Data. Un equipo basado en un modelo SIMD tiene N procesadores idénticos, cada uno con una memoria local propia, trabajando con una única secuencia de instrucciones.
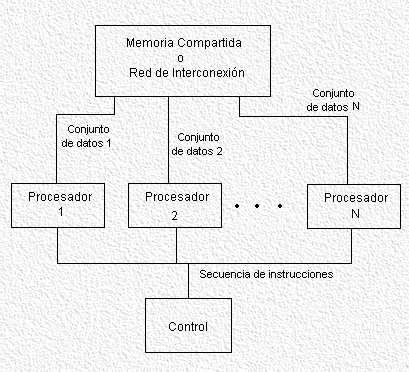
Todos los procesadores ejecutan la misma instrucción aunque sobre distintos datos.
En ocasiones puede ser necesario que sólo un subconjunto de procesadores ejecuten determinada instrucción, y será ésta misma instrucción la que lleve codificada si el procesador debe permanecer activo o inactivo. Los procesadores que queden inactivos deberán esperar a la siguiente instrucción.
Para la ejecución de las tareas es necesario que los procesadores puedan comunicarse, bien usando memoria compartida o una red de interconexión.
Este tipo de máquinas es también conocido como SM SIMD (Shared Memory Single Instruction Multiple Data), o como PRAM (Parallel Random Access Machine).
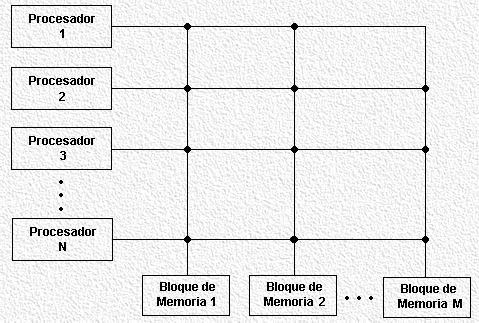
Se utiliza una memoria común para todos los procesadores, logrando que mediante ésta puedan comunicarse entre sí.
Los ordenadores SIMD se puede clasificar, según sus procesadores puedan acceder simultáneamente a una misma posición de memoria, en cuatro tipos:
En cualquier caso, la lectura simultánea no debe suponer ningún problema, pero no podemos decir lo mismo de la escritura. Para la resolución de conflictos de escritura se pueden utilizar varios criterios:
La mayoría de las máquinas siguen el primer modelo; EREW. El peor de los modelos para memoria compartida y tendremos que tenerlo en cuenta a la hora de diseñar un algoritmo ya que debemos evitar conflictos de acceso a memoria.
Tendremos entonces que tener en consideración el número de accesos múltiples que vamos a realizar sobre una misma dirección de memoria: o bien con todos los procesadores, o sólo un grupo de éstos.
N accesos múltiples, siendo N el número de procesadores. Si todos acceden a la misma dirección de memoria se utiliza un proceso de difusión:
Este proceso se va repitiendo hasta que los N procesadores conocen el contenido de la memoria.
Para realizar una escritura se utilizará un proceso equivalente que funcionará sólo si todos los procesadores pretenden escribir el mismo valor.
Este proceso se repite log N veces, conociendo entonces si se puede escribir o no en la memoria.
M accesos múltiples, siendo N el número de procesadores y M<N. Normalmente no va ha ser necesario que todos los procesadores accedan a una misma dirección de memoria. Si compartimos M posiciones de memoria asociamos a éstas 2N-2 palabras que formarán un árbol con N bifurcaciones, cada una asociada a un procesador, y que tiene por raíz de éste a la propia M.
Tanto para la lectura como para la escritura las solicitudes de los procesadores avanzan hacia la raíz de la misma forma que se hace para los N accesos múltiples (caso anterior).
Cada vez que un procesador accede a una posición de memoria necesita establecer un camino físico hasta ésta, lo que supone un aumento de coste en circuitería que podemos expresar como f(M). Si los N procesadores pueden acceder a esa posición de memoria, tendremos un coste total de Nxf(M), un coste que puede llegar a ser excesivo.
Una forma de abaratar la circuitería sería dividir la memoria compartida en R bloques de M/R posiciones, con lo que tendremos N+R líneas de doble dirección que permite acceder desde cualquier procesador a cualquier posición de memoria. Sin embargo sólo podrá hacerlo uno cada vez. Necesitaremos además un circuito decodificador para determinar la posición de memoria buscada. El coste total será entonces de NxR (circuitos decodificadores) más el coste de Rxf(M/R).
Se dividen las M posiciones de memoria entre los N procesadores, estando todos éstos conectados entre sí mediante una línea full duplex que permite la comunicación instantánea entre cualquier par de procesadores.
Necesitaremos por tanto:
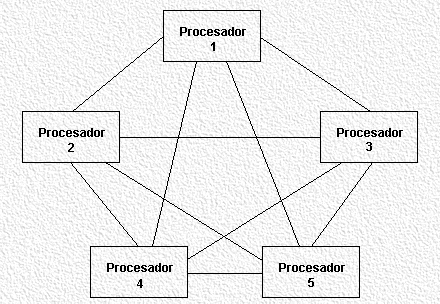
Este modelo conlleva una serie de problemas; por una parte existe un límite en el número de líneas que se pueden conectar a un procesador, y por otro el coste que supone esta red. Consideremos que de cada procesador saldrán N-1 líneas, y que por tanto la red tendrá un total de N(N_1)/2, lo que para un N grande supone un coste altísimo.
Además debemos recordar que este modelo sólo permite el acceso de un único procesador a una posición concreta de memoria en cada instante. Esto se podría resolver pero su coste sería de N2xf(M/N), un coste al que si añadimos el de las líneas full duplex que resulta más caro que el modelo SM SIMD (SIMD con memoria compartida).
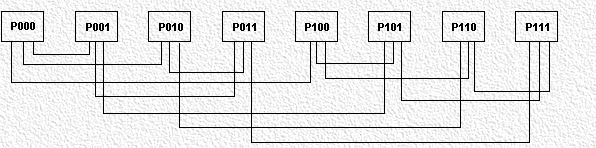
Las formas más comunes de redes de interconexión son las siguientes:

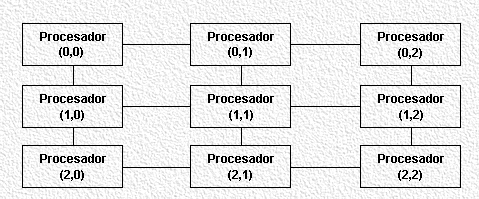

Se suelen usar líneas full-duplex.

Es el más general y potente de los ordenadores paralelos. Tenemos N programas distintos, N grupos de datos y N procesadores con una unidad de control, memoria local y sus unidades aritméticas y lógicas propios.
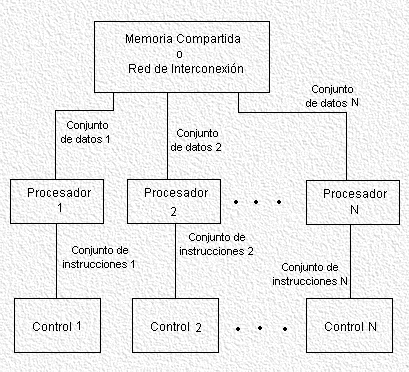
Cada procesador trabajará con las instrucciones que le envíe su unidad de control, por lo que los procesadores podrán utilizar programas diferentes sobre datos también diferentes. Los procesadores trabajan de forma asíncrona, y se comunican entre sí bien usando memoria compartida (multiprocesadores o máquinas de acoplamiento fuerte) o una red de interconexión (multiordenadores o máquinas de acoplamiento débil).
Si los procesadores se encuentran próximos entre sí se habla de un multiordenador, pero si se encuentran distantes hablamos de un sistema distribuido y entonces tendremos que tener en consideración el número de intercambios entre procesadores.
Los ordenadores MIMD se usan para resolver problemas con estructura irregular, más difíciles de diseñar, evaluar e implementar.
Un algoritmo asíncrono hace que una serie de procesos trabajen simultáneamente, e un algoritmo paralelo un procesador comienza los procesos que generan tareas que se ejecutan en otros procesadores. Estos procesos o tareas son asignados a procesadores desocupados. Si no hubiesen procesadores libres se incluiría la tarea en una cola de espera. Si por el contrario no hay suficientes tareas, se crea una cola de procesadores.
En teoría cualquier algoritmo paralelo puede ser ejecutado en un modelo MIMD, sin embargo la práctica más común es la de ensamblar procesadores de una forma de determinada para un problema en concreto, lo que hace que no sirva para otro tipo de problemas. A esto se le denomina arquitecturas especializadas.
![]()
Para determinar si un algoritmo es o no bueno debemos considerar su rapidez, su coste de ejecución y su eficiencia en el uso de los recursos disponibles. Se evalúan los siguientes criterios: tiempo de ejecución, número de procesadores usados y el coste.
Es el factor más importante en la evaluación. Se considera tiempo de ejecución el que necesita el algoritmo desde que éste comienza a funcionar en cualquier procesador, si no comienzan a trabajar todos los procesadores de forma simultánea, hasta que el último procesador termine su tarea.
Consiste en el análisis teórico del tiempo que necesita el algoritmo en resolver el problema en el peor de los casos. Se cuentan el número de operaciones básicas o pasos y se multiplican por el número de veces que serán ejecutadas, que dependerá del número de entradas que reciba en el peor caso.
Para obtener el tiempo de ejecución en un algoritmo paralelo debemos distinguir entre pasos computacionales y de encaminamiento. Los primeros son operaciones lógicas o aritméticas (una suma, asignación de una variable, etc...), los segundos se refieren al envío de datos de un procesador a otro a través de la memoria compartida o de la red de comunicación según corresponda.
El tiempo de ejecución dependerá por tanto del número de entradas como del número de procesadores.
Normalmente, se suelen comparar los nuevos algoritmos con otros ya existentes. Nos interesa que nuestro algoritmo sea rápido y esto se comprueba utilizando un límite inferior, que corresponde al número mínimo de pasos necesarios para solucionar el problema en el peor de los casos. Si el número de pasos del algoritmo coincide con el límite inferior se dice que el algoritmo es óptimo en lo que a rapidez se refiere.
Si el algoritmo es más rápido que ningún otro conocido se tiene un nuevo límite superior. Así pues el límite superior se considera al algoritmo más rápido resolviendo determinado problema en su peor caso.
Esto es en lo que se refiere a algoritmos secuenciales. Para algoritmos paralelos deberemos tener además en consideración otros factores:
Como antes hemos comentado, se suelen comparar los algoritmos con los mejores ya conocidos. Se suele evaluar un algoritmo paralelo en función a un algoritmo secuencial. Esta es una buena forma de conocer la mejora de velocidad. Recordemos que un algoritmo secuencial puede simularse con un ordenador secuencial: simulando primero a P1, luego a P2, y así sucesivamente. Con esto obtendremos la suma de los tiempos de los N procesadores, que será como máximo N por el tiempo que tardarían los procesadores en paralelo.
¿Que se deduce de esto?. En teoría debemos esperar que un proceso en paralelo tenga una velocidad equivalente a la de dividir lo que tarde un procesador paralelo entre N. Esto no va a ser así por dos motivos:
Es el segundo criterio en importancia. Es imprescindible conocer el número de procesadores que vamos a necesitar para resolver un problema, ya que a mayor número de éstos mayor será el coste del problema. Tendremos un coste de compra, de mantenimiento y un aumento de coste si buscamos un alto grado de fiabilidad.
No siempre el número de procesadores va a depender del volumen de la entrada, pero sí del tamaño del problema.
Se puede definir mediante el producto: tiempo de ejecución por número de procesadores usados. O lo que es lo mismo coste de los pasos dados por todos los procesadores para el caso peor.
Si el coste de un algoritmo paralelo es igual al limite inferior multiplicado por una constante tendremos un coste óptimo. Es decir que en lo que se refiere a coste el algoritmo no puede mejorarse. El coste no será óptimo si existe un algoritmo secuencial con tiempo de ejecución menor al coste del algoritmo paralelo.
Siempre nos queda la posibilidad de reducir el tiempo de ejecución añadiendo procesadores, o reducir el número de procesadores a cambio de un mayor tiempo de ejecución, y en ambos casos mantener el coste óptimo.
Si T(n) es un límite inferior al número de pasos secuenciales necesarios para determinado problema de tamaño n, T(n)/N es un límite inferior para el tiempo de ejecución de un algoritmo paralelo con N procesadores.
Si no se conoce ningún algoritmo secuencial óptimo que solucione el problema, se utilizará la eficiencia del algoritmo paralelo como medida para evaluar su coste. La eficiencia se mide como el tiempo de ejecución de un algoritmo secuencial (aunque no sea óptimo) para el peor de los casos respecto al coste del algoritmo paralelo. Si el valor resultante es mayor que 1 es que existe un algoritmo secuencial mejor que el que estamos usando para la evaluación.
Hoy en día la tecnología permite que lo que antes era un conjunto de puertas lógicas, se agrupen en chips capaces de contener varios procesadores. Esta tecnología ha venido unida al éxito de los ordenadores paralelos. Es la denominada VLSI (Very Large Scale Integration) que agrupa casi un millón de puertas en 1 cm2. Los algoritmos utilizados en los potentes ordenadores paralelos con tecnología VLSI tienen que tener en consideración otras medidas, además de las anteriores.
Lo que hace que el ordenador pueda crecer con mucha facilidad (sólo hay que añadir nuevos módulos). Como ventaja también podemos comentar el que el tiempo necesario para transmitir un dato de un procesador a otro es siempre constante. El tiempo requerido para una comunicación o encaminamiento, como antes se indicó, es una medida de evaluación del algoritmo, por tanto la longitud de los cables debe ser considerada como otra medida para algoritmos paralelos.